9.2 Index of Coincidence
The index of coincidence is a measure of how close a frequency distribution is to the uniform distribution. If you choose two letters at random from a random piece of text, the probability that they are the same is about 0.0385, whereas if you choose two letters at random from a piece of English text, the probability that they are the same if about 0.0667. This probability does not change if the text is enciphered with a substitution cipher. We can therefore exploit this phenomenon to decide if a given piece of ciphertext has been enciphered by a substitution cipher such as a Caesar shift.
Given a piece of text of length \(N\) in which the letters ‘A’ to ‘Z’ appear with frequency \(f_i\) (\(i=A\) to \(Z\)) then the index of coincidence of the text is defined as
\[IC=\frac{26\sum_{i=A}^Zf_i(f_i-1)}{N(N-1)}.\]
Note that some definitions omit the value 26 from the above definition.
If the text is essentially ‘random’ then the index of coincidence will be close to \(1\). If it is text written in English (and possibly enciphered using a substitution cipher) then it will be closer to \(1.734\) (\(= 26\times 0.0667\)).
We can exploit this when analysing a piece of ciphertext that we suspect has been encoded using a vigenère cipher. If we have a guess that the keylength is \(n\) then we can write the ciphertext using \(n\) columns and extract all \(n\) columns from the ciphertext. Given that each of these has been enciphered using a Caesar shift (with a different value for the shift), we can calculate the index of coincidence for each column and if these are (or better, their average is) close to \(1.734\), then there is a good chance that \(n\) really is the key length. If not, then we can try another value of \(n\).
For example the following text has been enciphered using a Vigenère cipher with the keyword CIPHERS
KVRYC GLQOG HTYQC KXWLV JQZRF TYWTQ HHRRD IWGPX YEHWG WIIXQ ZBPRX WPKGF TKAQV DYHVU TGEAM FFKVP ZIIAG ADMAV DNLTM MEWFA ILTJL JIIJE ETGND SPFOG LPZEG JQKTK YIWCV PSXVJ PIIPZ VDGAH JSDEQ VILVD AUMCJ MGZGZ BLRKL QMCJM GZGZD YIEUQ LTPWK GEWCC IILKV UVVDS VQDUM ELQKX WLVJQ ZRVHV LCSTU JIGOP IATJW PEXRM GWFQP VVXOK SXJMG ZGZ
If we calculate the index of coincidence based on the text having a key length of either 1 or 2 or 3 or 4 or … or 15, then we get the following chart
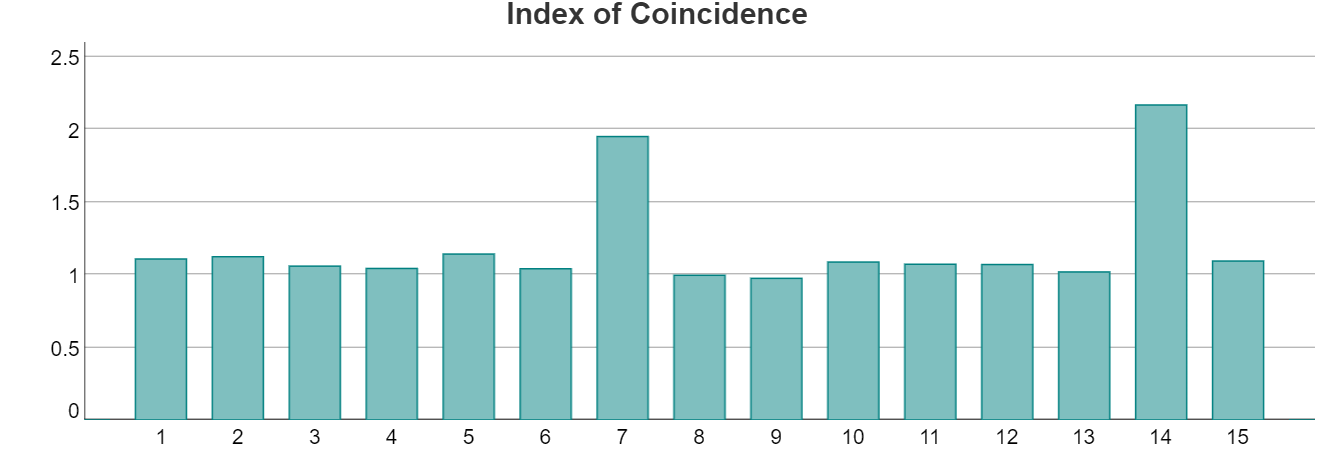
There is clearly a large ‘spike’ at the value 7 (and 14) which indicates that the length of the keyword is probably 7. Frequency analysis on the 7 columns can then be used to try to decipher the text.
(in case you are wondering, the plaintext is
In cryptography, a cipher (or cypher) is an algorithm for performing encryption or decryption in a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. To encipher or encode is to convert information into cipher or code. (taken from https://en.wikipedia.org/wiki/Cipher)
with all the non-alphabetic characters stripped out.)