Chapter 12 Appendix C - Infinite Cardinals
In Chapter 1, count the number of letters of the alphabet than have a dot above them (e.g) the letter “i”.
In Chapter 1, count the number of dots that have a letter of the alphabet below them.
Perhaps you didn’t go to the trouble of actually completing Exercise 12.1 but if you had it would probably have taken you quite a few minutes to complete. Exercise 12.2 on the other hand would have taken you, perhaps, half a second, to answer.
Solution. You intuitively know, that for every letter that has a dot above it, there is a corresponding dot that has a letter below it. Hence there is bijection between the set of letters with a dot above them, to the set of dots with a letter below them. You also know, intuitively, that any two finite sets with a bijection between them must have the same size. So if you have taken the trouble to calculate the size of one of these sets, you automatically know the size of the other.
Notice that the converse is true as well. If we have two finite sets of the same size, we can easily construct a bijection between them (in fact you should already know that if the size of these sets is \(n\) then there are \(n!\) distinct such bijections). The size of a set \(X\) is called the cardinality of the set and is denoted by \(|X|\). We use the previous observation to motivate the following definition.
Let \(X\) and \(Y\) be two sets (not necessarily finite). We say that \(X\) and \(Y\) have the same cardinality if and only if there exists a bijection \(X\to Y\).
Let \(\mathbb N,\mathbb Z, \mathbb Q\) denote the natural numbers, integers and rational numbers respectively and let \(2\mathbb N\) denote the even natural numbers. The following sets all have the same cardinality as \(\mathbb N\).
- \(2\mathbb N\);
- \(\mathbb Z\);
- \(\mathbb Q\).
Proof. In all cases, we show that there is a bijection between \(\mathbb N\) and the relevant set.
- The map \(\mathbb N\to2\mathbb N\) given by \(n\mapsto 2n\) is clearly a bijection.
- Consider the map \(\mathbb Z\to\mathbb N\) given by \(0\mapsto1\), \(n\mapsto 2n\), \(-n\mapsto2n+1\) for \(n\in\mathbb N\). It is easy to see this is a bijection.
- Consider first the set \(\mathbb Q^+\) of positive rationals. It is clear that each positive rational appears (at least once) in the following array
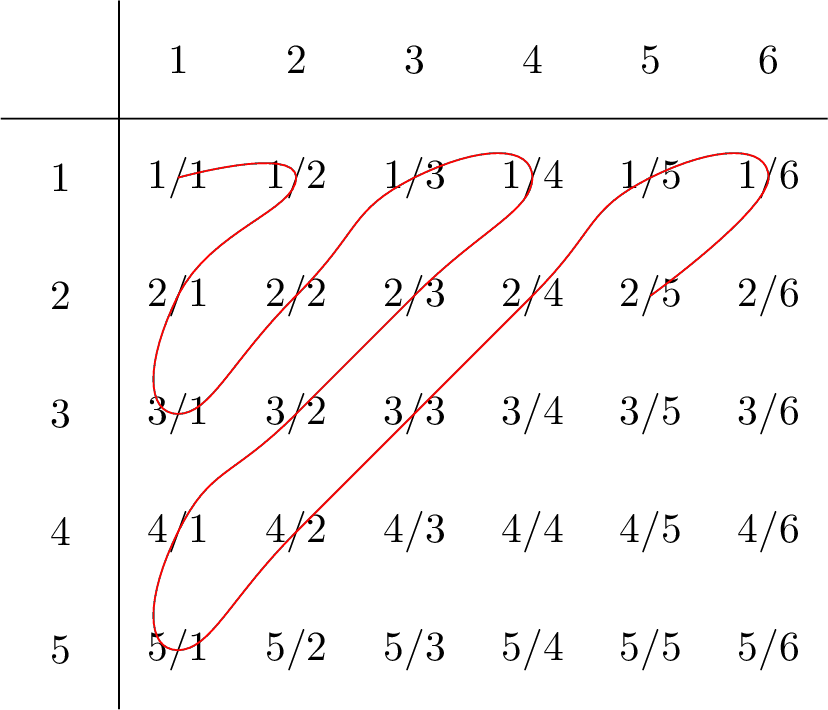We trace a diagonal path through this grid in the following order
\[
1/1\to1/2\to2/1\to3/1\to2/2\to1/3\to1/4\to2/3\to3/2\to4/1\to5/1\to\ldots
\]
each time we meet a rational number that has appeared previously (e.g. \(2/2 = 1/1\)) we ignore it. This then clearly generates a list that is in 1-1 correspondence with \(\mathbb N\) and so enables us to form a bijection \(\mathbb Q^+\to\mathbb N\). We can then easily extend this to a bijection \(\mathbb Q\to\mathbb N\) in a similar way to the bijection \(\mathbb Z\to\mathbb N\).
At this point, you may be forgiven for thinking that all infinite sets have the same cardinality. But they don’t.
There is no bijection \(\mathbb N\to(0,1)\),
Proof. We first make some observations regarding the interval \((0,1)\).
- All real numbers (in \((0,1)\)) have a decimal expansion.
- All real numbers (in \((0,1)\)) have an infinite decimal expansion; e.g. \(1/3 = 0.\dot{3}\), \(1/2 = 0.5\dot{0}\).
- Some real numbers have two decimal expansions. For example \(1/2 = 0.5\dot{0} = 0.4\dot{9}\).
Suppose now that there exists a bijection \(f : \mathbb N\to(0,1)\). Let us represent \(f(n)\) by the infinite decimal expansion \[ f(n) = 0.d_{n1}d_{n2}d_{n3}\ldots \] where \(d_{ni}\in\{0,\ldots,9\}\), and further agree that if \(f(n)\) is one of the values in observation (3) above then we never use the expansion that ends in an infinite number of \(9\)’s.
We obtain a contradiction by describing a number \(r\in(0,1)\) that is not in the image of the function \(f\). Consider then \[ r = 0.r_1r_2r_3\ldots \] where we define \[ r_i=\begin{cases}0&\text{if }d_{ii}\ne0\\1&\text{if }d_{ii}=0.\end{cases} \] It then follows that for all \(n\in\mathbb N\), \(r\) differs from \(f(n)\) in the \(n^\text{th}\) decimal place. Hence \(r\not\in\text{ im }(f)\) and so \(f\) cannot be a bijection.
This clearly means that \(\mathbb N\) and \((0,1)\) have different cardinalities. It can be shown that \((0,1)\) has the same cardinality as \(\mathbb R\). We normally denote the cardinality of \(\mathbb N\) as \(|\mathbb N| = \aleph_0\) (pronounced ‘aleph-nought’) and that of \(\mathbb R\) as \(|\mathbb R| = \aleph_1\).
The next result shows that there are infact an infinite number of infinite cardinalities!
Let \(X\) be a set and let \({\cal P}(X)\) be the power set of \(X\) (i.e. the set of subsets of \(X\)). Then \(|{\cal P}(X)|>|X|\).
Proof. Suppose that \(f:X\to{\cal P}(X)\) is a bijection and consider the subset of \(X\) defined by \[ S = \{x\in X| x\not\in f(x)\}. \] Since \(f\) is a bijection, there exists \(y\in X\) such that \(S = f(y)\). However, if \(y \in S\), then \(y\in f(y)\), which by the definition of \(S\) leads us to conclude that \(y\not\in S\), a contradiction. Hence we must have \(y\not\in S\). But then, from the definition of \(S\) we conclude that \(y\in f(y)\) and so \(y\in S\), another contradiction. Consequently, no such \(y\) exists and so \(f\) cannot be a bijection and we conclude that \(|X| < |{\cal P}(X)|\).