9.3 Chi-squared test
As an alternative to the index of coincidence, we can use a technique that is dependant on a statictical test, called the Chi-squared test. This is a measure of how similar a distribution is to the expected values for that type of distribution. In cryptography we define the Chi-squared statistic as \[ \chi^2(C,E) = \sum_{i=A}^{i=Z}{\frac{(C_i-E_i)^2}{E_i}} \] where \(C_i\) is the actual count of the letter represented by \(i\) in our text, while \(E_i\) is the expected count (taking account of the expected frequency of letters from whichever natural language the text is taken from - in our case, normally English) (in the table below, we ‘normalize’ the values by dividing by \(n\), where \(n\) is the length of the text). In essence, the smaller the Chi-squared statistic, the more likely it is to have been written in English.
As an example, the text
FTQNQ EFWUZ PEARB QABXQ MDQIM DYMZP WUZPF TQKMD QMXIM KEFTQ DQMZP FTQKZ QHQDY UZPFT QNQEF WUZPE ARBQA BXQEY UXQMZ PQYND MOQFT QKEGB BADFK AGIUF TEFDQ ZSFTM ZPSDM OQ
is the output of a caesar shift. By considering all possible shift values, we can see that the lowest chi-squared statistic occurs for a shift of 12, suggesting that this is the shift used.
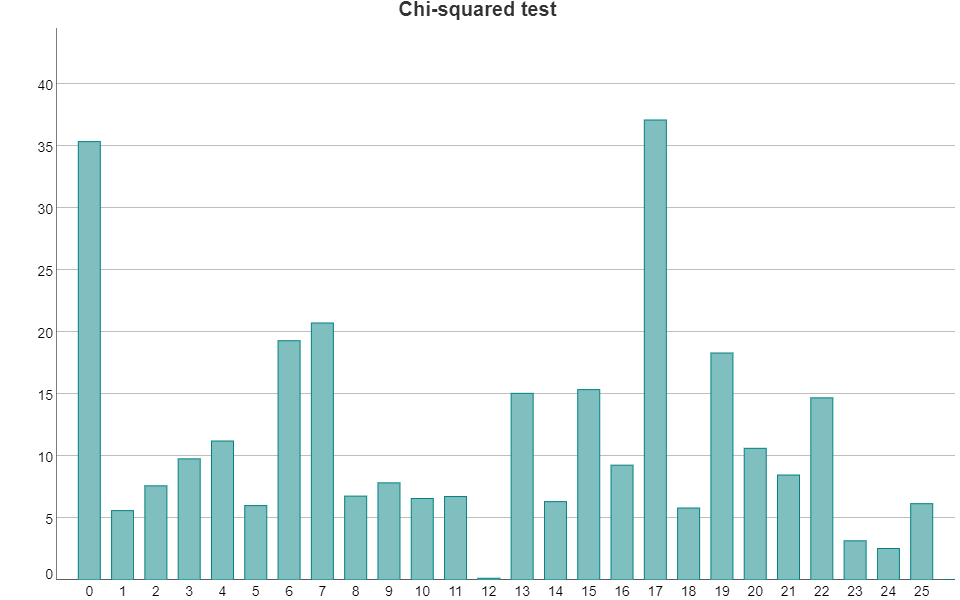 I leave it as an exercise for you to decipher the text.
I leave it as an exercise for you to decipher the text.