9.4 Frequency Analysis
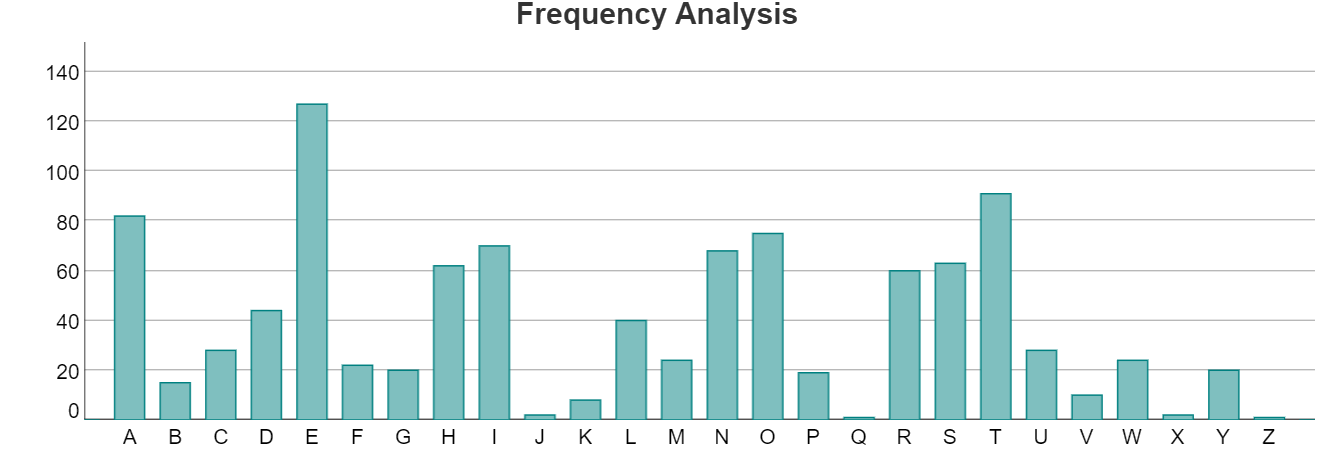
If you encipher a plaintext message using a substitution cipher then the letters in the ciphertext will occur with the corresponding frequency of their plaintext values. This information enables us to attack the ciphertext using frequency analysis. One counts the number of occurrences of each character in the ciphertext and compares it with an expected frequency for the standard English alphabet.
For example if we consider the following text which has been enciphered using a Caesar shift cipher
FHHTW INSLY TXZJY TSNZX HFJXF WXNRU QDWJU QFHJI JFHMQ JYYJW NSFRJ XXFLJ BNYMY MJQJY YJWYM FYNXY MWJJU QFHJX KZWYM JWITB SYMJF QUMFG JYHWD UYTLW FUMJW XTKYJ SYMNS PNSYJ WRXTK YMJUQ FNSYJ CYFQU MFGJY FXGJN SLYMJ FQUMF GJYZX JIYTB WNYJY MJTWN LNSFQ RJXXF LJFSI YMJHN UMJWY JCYFQ UMFGJ YFXGJ NSLYM JQJYY JWXYM FYFWJ XZGXY NYZYJ INSUQ FHJTK YMJUQ FNSQJ YYJWX BMJSY MJUQF NSYJC YFQUM FGJYN XUQFH JIFGT AJYMJ HNUMJ WYJCY FQUMF GJYFX XMTBS GJQTB NYNXH QJFWY TXJJY MFYYM JHNUM JWYJC YFQUM FGJYM FXGJJ SXMNK YJIGD YMWJJ UQFHJ XMJSH JYMNX KTWRT KXZGX YNYZY NTSNX TKYJS HFQQJ IYMJH FJXFW XMNKY HNUMJ WFHNU MJWNX YMJSF RJLNA JSYTF SDKTW RTKHW DUYTL WFUMN HXZGX YNYZY NTSNS BMNHM JFHMQ JYYJW NXWJU QFHJI GDFST YMJWQ JYYJW TWXDR GTQYM NXYJC YNXYF PJSKW TRMYY UBBBX NRTSX NSLMS JYYMJ GQFHP HMFRG JWHFJ XFWMY RQ
The individual characters appear with the following frequencies
We can compare this to the chart above and guess that the letter E, the most popular letter in English text, is encoded as J which would give a shift value of 5. This is indeed correct.
ASINTOER Frequency
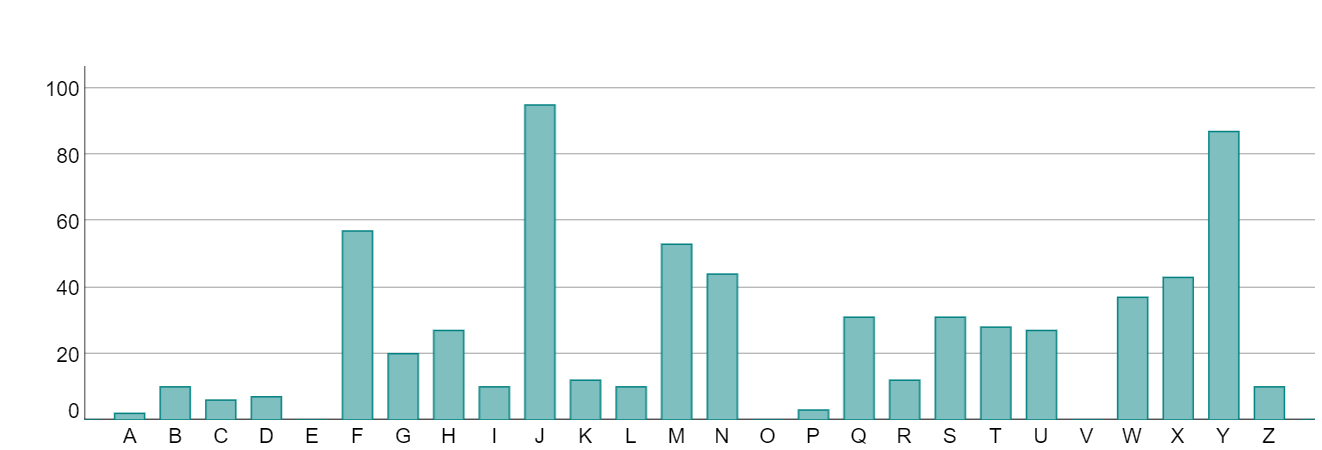
Indeed, if we take any substring in the ciphertext, say for example every second character, then the letter frequencies for this substring should be approximately the same as for the original string. For example, taking every 4th character in the previous ciphertext, starting at character 4, we get
TSXTX XNDQI MYSXJ MQJFY JHZJB JMYUW JKYPJ TJNCU JGLFF ZYNMN FXJYN WYMYJ YJWFJ XZNFK USYBY QYFFN FFJHJ CUJXS TNJTY YNWYM YGXYD JFMJX RZNNX JQYFW KUFMX SLSSW HYFHX ZSMJQ JWFGT WYWGM JXJTY BTSJJ HFWXY
with frequency table
The letter J is still the most frequent character by a long way and the two charts are very similar in nature. We could reasonably guess from this that the shift was 5.
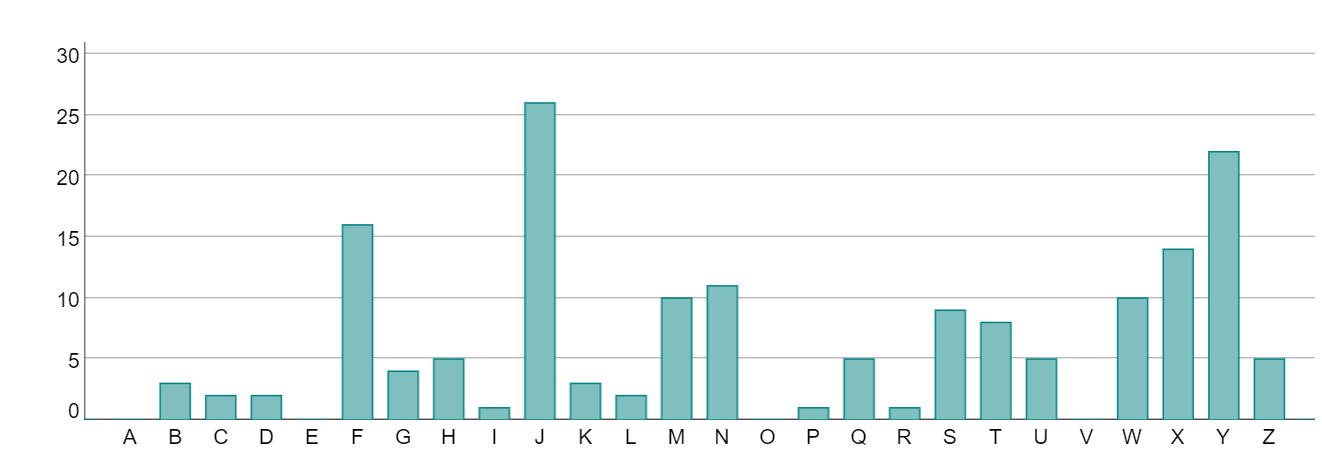
However, this does not always hold. For example, taking every 5th character in the string above starting at character 3, we get
HSZNJ NWHHY FFYQW NJHWI MMHTM KMSXJ SFGGY UYYYT SXFJJ YFXLJ XFGZS JJSJJ UYQJQ FYUJU YTQNF JYNYQ JGMIW FJMWZ YSYQM XNUHW JLYKK YUZYS NHYWH FJYXQ YXSMB TLYFF HW
with frequency table
The frequency chart is a little bit different to the previous one, and the most frequent character now is Y, which would give a shift value of 20.
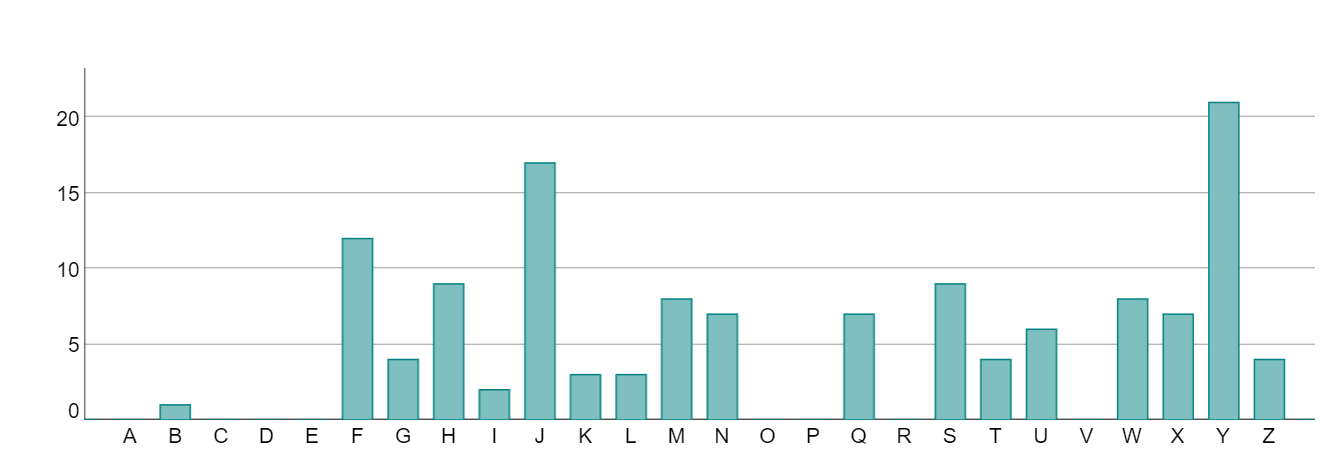
In this case, instead of just considering the single most common letter in English, we can consider multiple letters at the same time. For example, 8 of the most common letters in the English language are E, T, A, O, I, N, S and R. In the following chart, we have considered each of the 26 possible shift values (0 - 25) and calculated the sum of the frequencies of the enciphered values of the five letters E, T, A, O, I, N, S and R (we use the mnemonic A SIN TO ER to remember these).
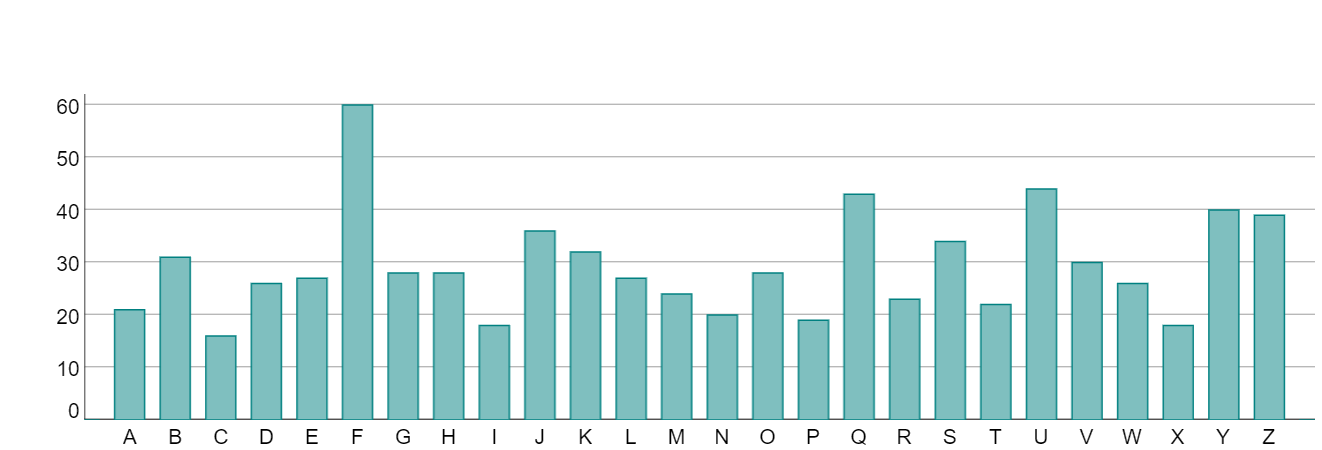
It is then clear that the highest aggregate frequency occurs for a shift of 5, confirming the shift value for the original text. This technique can be particularly useful when deciphering the Vigenère cipher. Note however that it might not always be accurate! You have to be prepared to use some trial and error when analysing a ciphertext.
In Appendix H we have set up a form to encrypt and decrypt Vigenère ciphers and added a version of a cracking algorithm for you to play with. In our algorithm we use the index of coincidence to ‘guess’ the length of the keyword (calculate the index of coincidence for lots of possible keylengths and then choose the ‘best’), and then use ASINTOER frequency analysis to determine the shifted value for each column, and so recover the keyword.