8.2 Digital Signatures
Cryptographic signatures/digital certificates
This system also gives a way of signing a message, to prove to a receiver that it comes from you and from nobody else.
The fundamental problem with digital signatures is the question of how you stop them being cut and paste from one document you did send onto another one you didn’t. Once this problem is solved (which is done using hash functions, described below) the idea is to turn public key encryption on its head, publishing a decryption key that everyone knows and keeping secret an encryption key.
Digests
The first stage in digitally signing the document is to produce a so called digest (also known as a hash), that is, a short summary of the document, typically 1024 bits long. The method of producing the digest varies between the different secure signature systems, but it is an algorithm chosen to make it unlikely that two different messages will produce the same digest. This digest is attached to the message and proves that it has not been tampered with.
So long as the message and its digest match we have reason to believe the message is authentic.
But the digest algorithm is public so anyone tampering with the message just has to also replace the digest too. To prevent that, the digest is encrypted using the secret encryption algorithm.
Verifying the message
On receipt of the message the recipient deciphers the digest using the published decryption key, and then uses the digest algorithm to produce their own version of the message digest directly from the message contents. If the decrypted digest matches the new one then the signature and the message (almost certainly) belong together and the message is genuine. The security of these systems relies in part on the reliability of the digest used.
The Birthday Attack
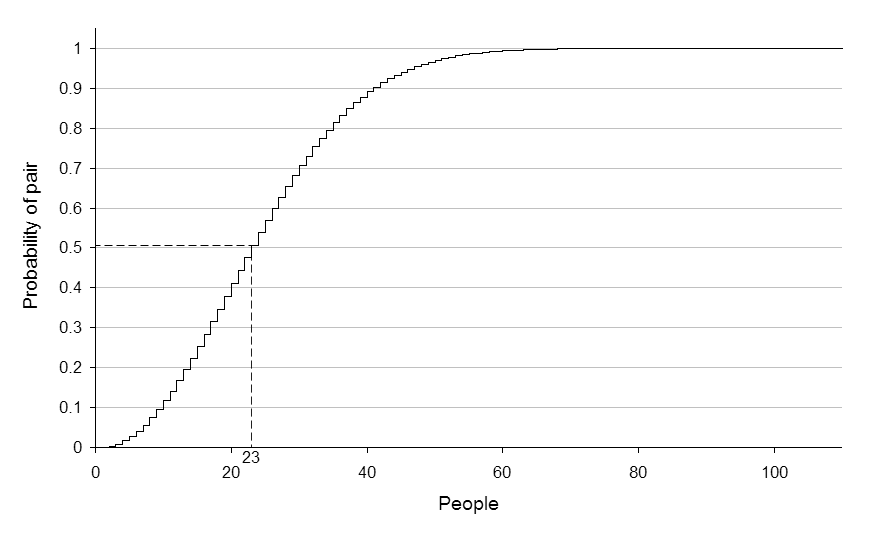
This is a method to circumvent digital signatures based on the Birthday paradox. The classical birthday paradox states that in a group of 23 people there is a probability of 1/2 that at least two of them share the same birthday. In a larger group the odds are even higher.
Assuming that birth dates are uniformly distributed (actually they are not) and ignoring leap years there are 365 possible birthday dates. Consider all the possible collections of birthdays assuming that no two people in a group of size \(n\) share a birthday.
The first person in the group has 365 possible birthdays, the second has 364 and so on. Hence there are \(365!/(365-n)!\) possibilities for the list of birthdays, so the probability that no two people share a birthday is:
\[ \frac{365!/(365-n)!}{365^n}. \]
It follows that the probability that at least two people have a shared birthday is
\[ 1-\frac{365!/(365-n)!}{365^n}. \]
Attacking the digital signature
The security of the digital signature depends on the assumption that different messages have different hashes. If you have a large collection of messages then, as with birthdays, the odds that two messages have the same hash is higher than you might think. The birthday attack exploits this weakness.
If a 64 bit hash is used, that is each message is converted to a digest which is stored as a binary number with 64 digits, there are \(2^{64}\) (or approximately \(1.8 \times 10^{19}\)) different digests. If these are all equally probable (the best case), then given only \(5.1 \times 10^9\) different messages there is a probability of more than \(0.5\) that two of them have the same digest. We say that we have a probability of more than \(1/2\) of generating a collision.
The attack in practice
Alice wants to get Bob to sell his house for five pounds. She needs to get his digital signature on a contract to this effect. She produces a fair contract in which he agrees to sell his house for, say, three hundred and fifty thousand pounds, and an unfair contract in which he agrees to sell for five pounds.
She now pads the two contracts by adding spaces, punctuation and florid legal phrases in lots of different ways producing an enormous number of fair and of unfair contracts. Eventually she hopes a version (contract A) of the fair contract will have the same hash as some version (contract B) of the unfair contract. This is slightly different from the true Birthday paradox and the calculation is more delicate, but essentially the same idea works.
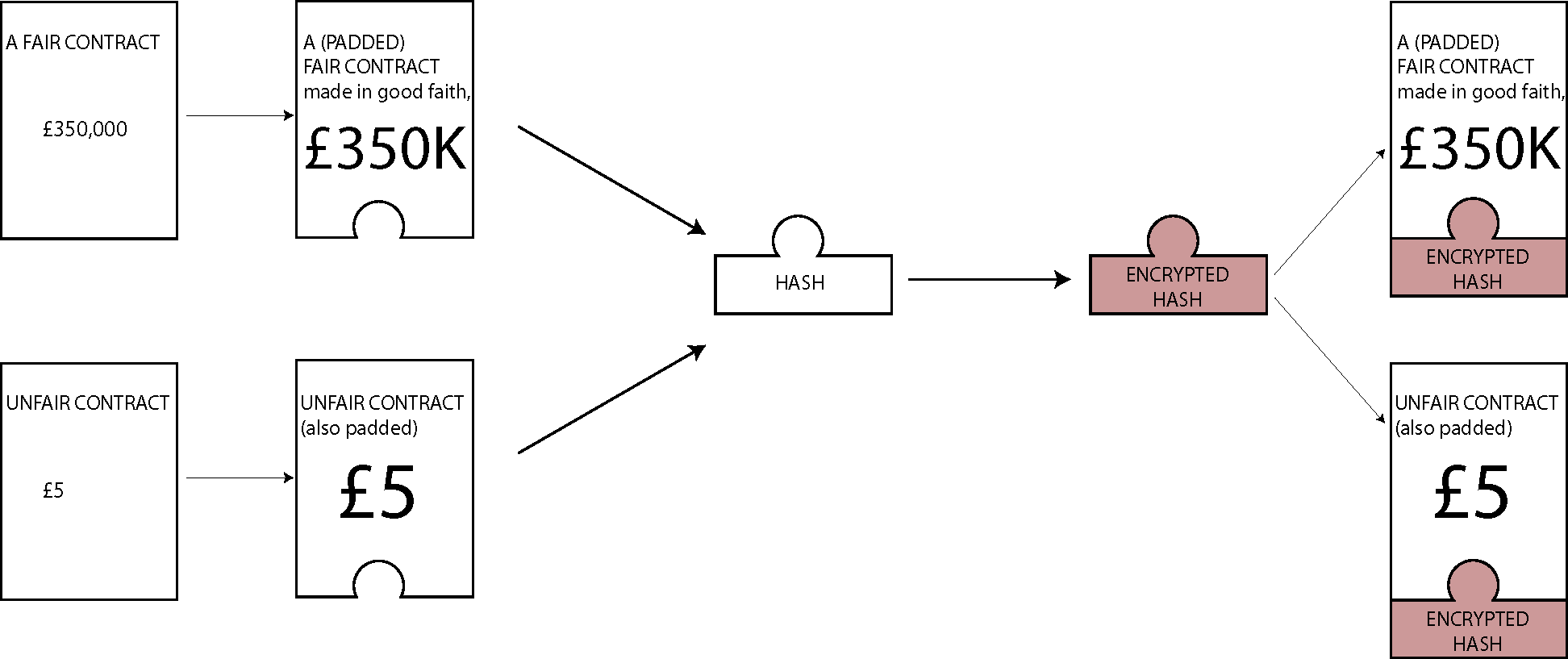
In practice this does not mean that Alice can force Bob to sell the house for five pounds. If she tries to do so Bob can produce the fair contract, and show that his signature fits it too. The real importance of the attack is that once it has been exhibited the signature system is no longer regarded as fully trustworthy.
Modern digital signature keys are chosen to be so long that even this attack is infeasible. Nonetheless the calculations of feasibility rely on the assumption that hash values are evenly distributed. This assumption may be false among the space of messages to be hashed, and at the CRYPT2004 conference collisions were announced in the widely used SHA-0, MD4, MD5, HAVAL-128, and RIPEMD hash algorithms.
Weakening the discrete logarithm
The same paradox weakens discrete log encryption. Recall that the security of the system relies on the fact that it is hard to find a value \(n\) such that \(y=x^n\text{ mod}~(p)\). Trying a brute force attack we would expect to need to test around \(p/2\) values of \(n\) to have a \(50\%\) chance of finding the correct value.
Instead we can compute values of \(x^r\) and \(yx^{-s}\). Because of the birthday paradox it takes only about \(1.2\sqrt p\) steps on average to find a pair \(x^r=yx^{-s}\) and so \(y=x^{r+s}\) solving the discrete log problem.
Note that computationally we have traded time for storage. The programme we write to implement such an attack will not take as long as a brute force attack to run, however it will need a lot of storage (Hard disc or RAM) in which to store the values of \(x^r\) and \(yx^{-s}\) for comparison. This trade off, of time against space, is a common one in algorithm design.