Chapter 9 More cryptography
In this section, we shall consider some more classic ciphers, sometimes referred to as ‘pen-and-paper’ ciphers. We have seen two such ciphers in the previous section, namely the Caesar shift cipher and the Affine shift cipher.
We are particularly interested in the cryptanalysis of these ciphers and how we might be able to crack an enciphered message with only minimal information relating to the key.
Keyword Substitution Ciphers
We have already seen a number of ciphers that are reasonably easy to attack. First of all the Caesar shift cipher (\(x\mapsto x+s\text{ mod}(26)\)) and then the Affine shift cipher (\(x\mapsto sx+t\text{ mod}(26)\)). Both of these ciphers are relatively easy to attack using frequency analysis. For the Caesar cipher, knowledge of the enciphered value of 1 character allows us to decipher the entire text, whilst for the Affine cipher, we only need to know the enciphered value of 2 characters.
The Caesar shift and Affine shift ciphers are examples of simple substitution ciphers, where each letter of our alphabet is replaced, or substituted, by a unique other letter.
| plaintext | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S… |
| ciphertext | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V… |
The drawback with the Caesar or Affine shifts, is that once we know one (or two in the case of Affine) substituted value, we can calculate them all. Ideally we would be better to have a completely random set of substituted values
| plaintext | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S… |
| ciphertext | X | P | R | A | Z | Q | K | N | S | D | T | H | E | F | W | O | I | Y | U… |
The problem with this is that for the sender and receiver to remember the randomised allocation, will be very difficult.
The solution is to use a keyword. Suppose we choose the keyword NUMBER, we construct our allocation as follows
| plaintext | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S… |
| ciphertext | N | U | M | B | E | R | S | T | V | W | X | Y | Z | A | C | D | F | G | H… |
List the distinct letters of the keyword, followed by all the rest of the letters, starting from the first unused letter after the final letter of the keyword. To reproduce the entire key, we would only need to remember the keyword. In order to decipher this type of cipher we would need knowledge of all (or at least a large number of) substitutions.
For example, if we encipher the plaintext
The best kinds of people are warm and kind. They are always there and they never mind. The best kinds of people smile and embrace. They support you with strength and grace.
with the keyword NUMBER we arrive at the ciphertext
ITEUE HIXVA BHCRD ECDYE NGELN GZNAB XVABI TEPNG ENYLN PHITE GENAB ITEPA EKEGZ VABIT EUEHI XVABH CRDEC DYEHZ VYENA BEZUG NMEIT EPHJD DCGIP CJLVI THIGE ASITN ABSGN ME
which has frequency table
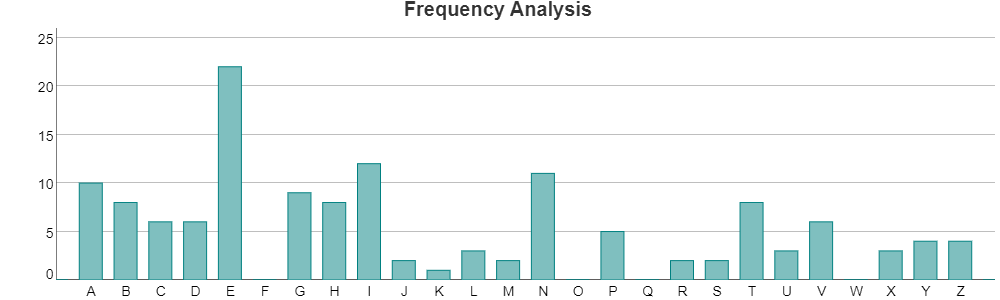
and although we could guess that ‘E’ has been enciphered as an ‘E’, it isn’t obvious what the other parts of the key are.
We will briefly look at attacking a substitution cipher later.
Vigenère Cipher
Successful use of frequency analysis with the Caesar and Affine shifts ciphers relies on the fact that each occurrence of each character in the plaintext, uses the same function to encipher it. This is an inherent weakness of the cipher and one that we would be best to avoid. It would be more useful from a cryptographic point of view, if we could encipher characters in a different way each time we met them in the plaintext. What if we could develop a technique to encipher some plaintext, where we use a different shift for each character? For example, if we used a Caesar shift with shift value of 5 on the plaintext
The best kinds of people are warm and kind. They are always there and they never mind. The best kinds of people smile and embrace. They support you with strength and grace.
we arrive at the ciphertext
YMJGJ XYPNS IXTKU JTUQJ FWJBF WRFSI PNSIY MJDFW JFQBF DXYMJ WJFSI YMJDS JAJWR NSIYM JGJXY PNSIX TKUJT UQJXR NQJFS IJRGW FHJYM JDXZU UTWYD TZBNY MXYWJ SLYMF SILWF HJ
which has frequency table
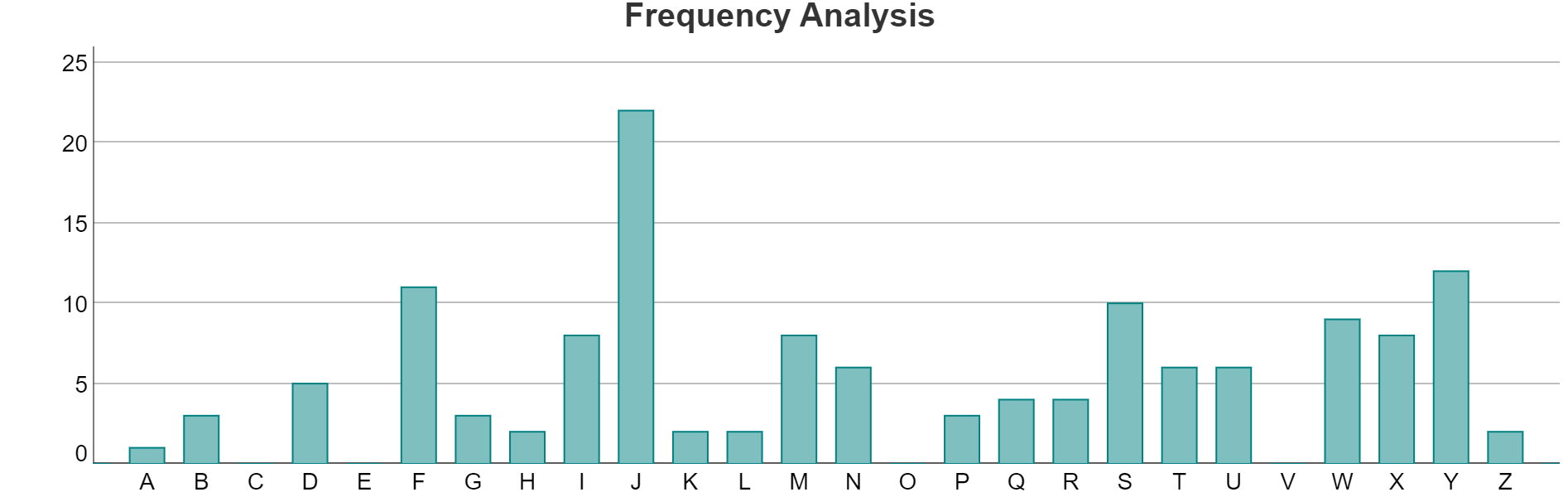
We could reasonably guess that the shift used was 5 as the most frequent character is now J.
Suppose instead we use the same plaintext but use the sequence of shift values
19 7 4 1 4 18 19 10 8 13 3 18 14 5 15 4 14 15 11 4 0 17 4 22 0 17 12 0 13 3 10 8 13 3 19 7 4 24 0 17 4 0 11 22 0 24 18 19 7 4 17 4 0 13 3 19 7 4 24 13 4 21 4 17 12 8 13 3 19 7 4 1 4 18 19 10 8 13 3 18 14 5 15 4 14 15 11 4 18 12 8 11 4 0 13 3 4 12 1 17 0 2 4 19 7 4 24 18 20 15 15 14 17 19 24 14 20 22 8 19 7 18 19 17 4 13 6 19 7 0 13 3 6 17 0 2 4
(that is we shift the first character by 19, the second by 7 etc)
we arrive at the ciphertext
MOICI KMUQA GKCKE ICEWI AIISA IYAAG UQAGM OIWAI IAWSA WKMOI IIAAG MOIWA IQIIY QAGMO ICIKM UQAGK CKEIC EWIKY QWIAA GIYCI AEIMO IWKOE ECIMW COSQM OKMII AMMOA AGMIA EI
which has frequency table
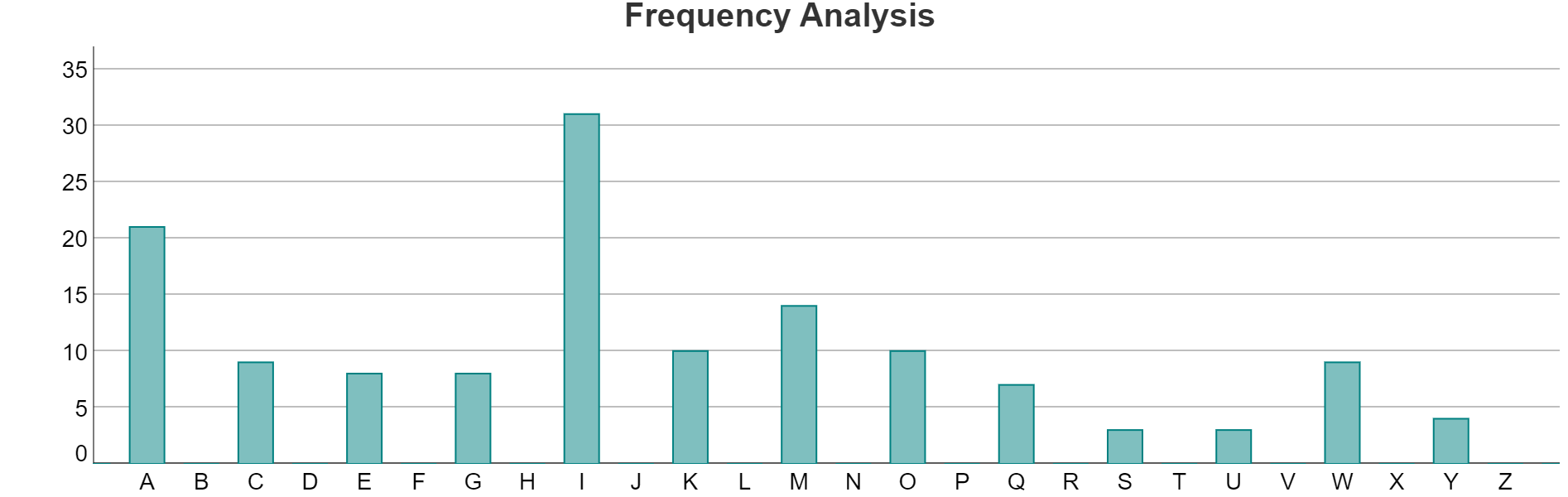
This is very different and it is not at all clear how we can use frequency analysis to decipher the ciphertext.
However, there is an obvious problem! How on earth do we (and the intended recipient) remember the sequence of shift values we need to use? The solution is to use a keyword or a keyphrase.
As with the keyword substitution ciphers, we pick a memorable keyword or a keyphrase, and we use the numerical values of the characters (A=0, B=1, etc) as the shift value for the corresponding letter.
For the example above, the keyphrase was
THE BEST KINDS OF PEOPLE ARE WARM AND KIND. THEY ARE ALWAYS THERE AND THEY NEVER MINDTHE BEST KINDS OF PEOPLE SMILE AND EMBRACETHEY SUPPORT YOU WITH STRENGTH AND GRACE
(this is not a very sensible choice of key, for obvious reasons!) and the corresponding numerical values were
19 7 4 1 4 18 19 10 8 13 3 18 14 5 15 4 14 15 11 4 0 17 4 22 0 17 12 0 13 3 10 8 13 3 19 7 4 24 0 17 4 0 11 22 0 24 18 19 7 4 17 4 0 13 3 19 7 4 24 13 4 21 4 17 12 8 13 3 19 7 4 1 4 18 19 10 8 13 3 18 14 5 15 4 14 15 11 4 18 12 8 11 4 0 13 3 4 12 1 17 0 2 4 19 7 4 24 18 20 15 15 14 17 19 24 14 20 22 8 19 7 18 19 17 4 13 6 19 7 0 13 3 6 17 0 2 4
Of course in general we would normally use a much smaller keyphrase that is shorter then the length of the original plaintext!
Suppose we had used the keyword Caesar on the text
According to Suetonius, Caesar simply replaced each letter in a message with the letter that is three places further down the alphabet. Cryptographers often think in terms of the plaintext alphabet as being the alphabet used to write the original message, and the ciphertext alphabet as being the letters that are substituted in place of the plain letters. When the plaintext alphabet is placed above the ciphertext alphabet, as shown below, it is clear to see that the ciphertext alphabet has been shifted by three places. Hence this form of substitution is often called the Caesar Shift Cipher. A cipher is the name given to any form of cryptographic substitution, in which each letter is replaced by another letter or symbol.
The shift values we would then use are
2 0 4 18 0 17
and we simply repeat this pattern as often as necessary.
2 0 4 18 0 17 2 0 4 18 0 17 2 0 4 18 0 17 2 0 4 18 0 17 …….
We arrive at the ciphertext
CCGGR UKNKL OJWEX GNZWS GSEJC RWAMG NYVWP CCCIV EREHP WTKGR MFADG SWSGV YIXZT YGLIL TVTTL STZUT LJEVR LEUEJ HUVLH VTDSO NKJEE DPYCB ILCIA PXGGI CPLWR JQFXW NKJIR CIEVE VESFH TLWPC CIRLE OVAPH HRDEX SSSGI RYTYG APHHR DEXMS VFTSO RZVEX ZEFTI KANRN MIKSR IEEFD KJEGA PYGRX WXKCL TZASG TEKBV KNKLH VNEXL EIUTL STRTE WMBJV IXMTV FIRHL REESX TYGPP SIENE XLEIU WLWNK JETDA ZPTIP TRNPL SBVVI WHLRE EHSBF XEXZE TKPLW RKGXX SLGJA FWTRU SLGWE DEPGW ZVIWU LVCRX GSVGT LSTKJ EGAPY GRXWX KCLTZ ASGTL SSSGE RKHZH TIVBP VHVWE GNAGW SYGNG WTYKS JGRDQ FWMBJ VIXMT ZQNMK OWVER UACNE HLHVE AIKAI UHMXT TKPLW RREIT ZEIKS XZEEC MIYIM GNXGA EAFSJ MFHCV QPKQG VSPYK CWMBJ VIXMT ZQNMF WYKCL WATJL ILTVT IWJEG NAGWD SAARG TYGRP WTKGR SJSPO BSDTY KSXWX KKSXS KVPFV GMYVT TOWNU IQGNJ KNKZN VVTLW BCCCO UHROB IJCRG SEJHK OL
with frequency table
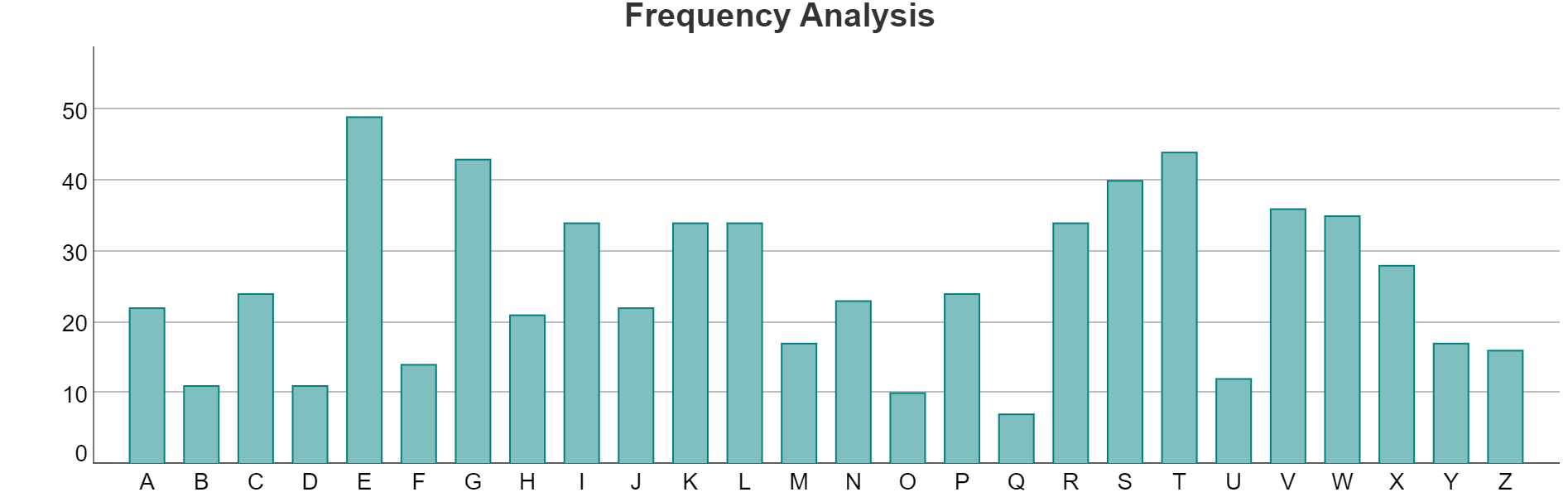
To assist the process we can make use of the following table:

This is known as a tabula recta. The letters in the first row correspond to the letters in the plaintext, while the letters in the first column correspond to the letters in the keyphrase.
For each letter in the keyphrase, lookup the corresponding row in the tabula recta and then look along for the corresponding letter in the plaintext
| PLAINTEXT | A | C | C | O | R | D | I | N | G | T | O | S | …. |
| KEYPHRASE | C | A | E | S | A | R | C | A | E | S | A | R | … |
| CIPHERTEXT | C | C | G | G | R | U | K | N | K | L | O | J | … |
In practice you may find it easier to split your plaintext into columns - 1 column for each letter of the keyword.
| C | A | E | S | A | R |
|---|---|---|---|---|---|
| A | C | C | O | R | D |
| I | N | G | T | O | S |
| U | E | T | O | N | I |
| U | S | C | A | E | S |
| A | R | S | I | M | P |
| L | Y | R | E | P | L |
| A | C | E | D | E | A |
| C | H | L | E | T | T |
| E | R | I | N | A | M |
| E | S | S | A | G | E |
| W | I | T | H | T | H |
| E | L | E | T | T | E |
| R | T | H | A | T | I |
| S | T | H | R | E | E |
| P | L | A | C | E | S |
| F | U | R | T | H | E |
| R | D | O | W | N | T |
| H | E | A | L | P | H |
| A | B | E | T |
Each column is then enciphered using the same Caesar shift, the value of which is given by the encoded value of the corresponding character in the keyphrase.
This type of cipher is known as a Vigenère Cipher, named after Blaise de Vigenère, who published a description of a similar cipher in 1586. The actual cipher we have described was really invented by Giovan Battista Bellaso, who built on the work of Leon Battista Alberti and Johannes Trithemius. It is an example of what is referred to as a polyalphabetic cipher where multiple substitution alphabets are used.
Keyword Transposition Ciphers
With a transposition cipher, rather than replace characters by other characters according to some rule, we simply transpose the order of the characters in the plaintext. Hence the ciphertext becomes simply a permutation of the plaintext. A simple example of this is the scytale that we saw at the start of Chapter 8. A more sophisticated example uses a keyword in the following way:
- Choose a keyword (e.g. TRANSPOSITION) and strip off any repeated letters (e.g. TRANSPOI)
- Form a grid with the reduced keyword in the first row and then the rest of the plaintext in the subsequent rows. E.g.
| T | R | A | N | S | P | O | I |
|---|---|---|---|---|---|---|---|
| A | C | C | O | R | D | I | N |
| G | T | O | S | U | E | T | O |
| N | I | U | S | C | A | E | S |
| A | R | S | I | M | P | L | Y |
| R | E | P | L | A | C | E | D |
| E | A | C | H | L | E | T | T |
| E | R | I | N | A | M | E | S |
| S | A | G | E | W | I | T | H |
| T | H | E | L | E | T | T | E |
| R | T | H | A | T | I | S | T |
| H | R | E | E | P | L | A | C |
| E | S | F | U | R | T | H | E |
| R | D | O | W | N | T | H | E |
| A | L | P | H | A | B | E | T |
- If the plaintext does not fit into the grid exactly, then we can, optionally, use ‘padding characters’ to fill in any gaps at the end.
- Now read down each column in turn, starting with the column whose first letter (i.e. the letter from the keyword) comes first in the alphabet and then proceeding alphabetically from then on.
Using the above example, we get the ciphertext
COUSP CIGEH EFOPN OSYDT SHETC EETOS SILHN ELAEU WHITE LETET TSAHH EDEAP CEMIT ILTTB CTIRE ARAHT RSDLR UCMAL AWETP RNAAG NAREE STRHE RA