Chapter 8 Applications to cryptography
Secret ciphers have been used since ancient times to send messages securely, for instance in times of war or diplomatic tension.
Nowadays sensitive information of a medical or financial nature is often stored in computers, and it is important to keep it secret.
Throughout this section, we shall assume that the alphabet that we are working with only consists of the upper case letters A,B,\(\ldots\),Z.
Caesar shift ciphers
Figure 8.1: Julius Caesar
the letters as integers, say A=\(0\), B=\(1\), \(\ldots\), Z=\(25\), and then adding \(1\) to each. In order to encipher Z as A, we must add \(\text{mod}~(26)\), so that \(25+1\equiv 0\). Similar ciphers are obtained by adding some fixed integer \(k\) (known as the key), rather than \(1\): Julius Caesar used the key \(k=3\). To decipher, we simply apply the reverse transformation, subtracting \(k\text{ mod }~(26)\).
Frequency Analysis
There are two problems with the Caesar Shift cipher. The first is that the key space is small. There are only 25 non-trivial values for the key and we can easily exhaust all values in order to test which one was actually used.
The second problem concerns frequency analysis. In an ‘average’ piece of English language text, the letters tend to appear with a definite frequency. The letter ‘E’ is usually the most frequent, followed by the letter ‘T’, then ‘A’ and so on.
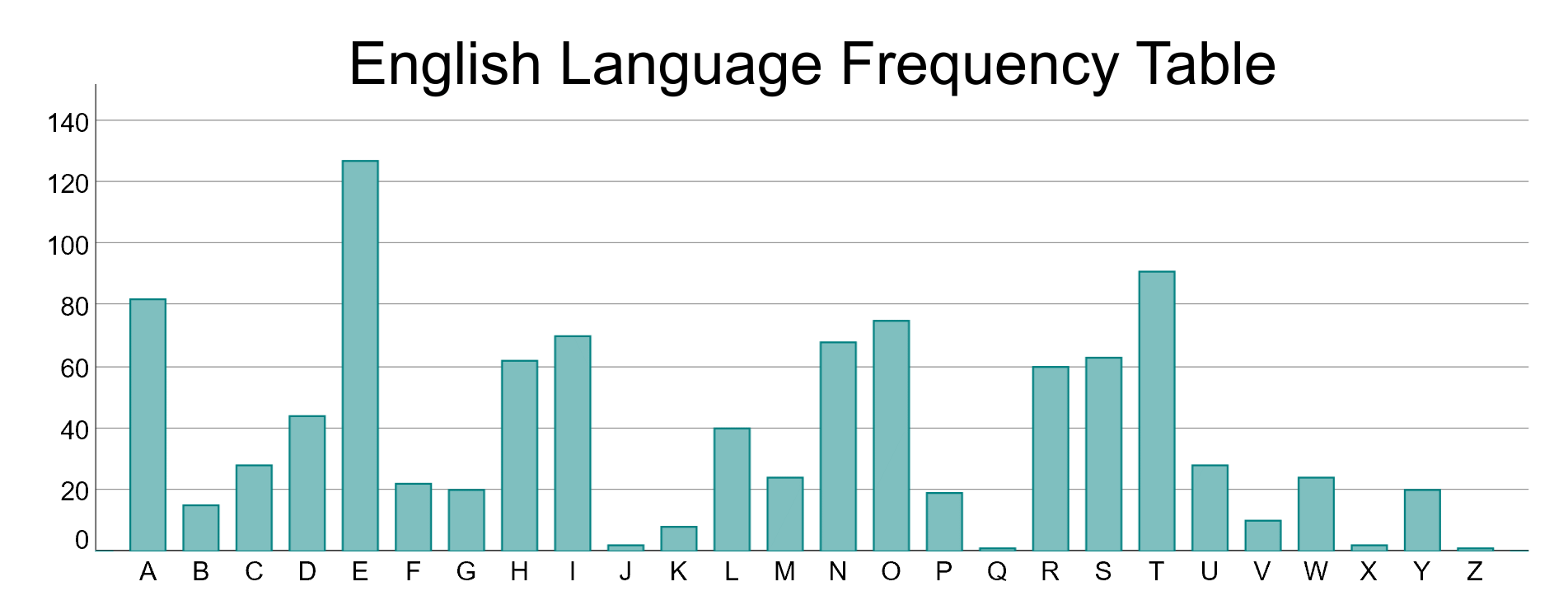
If we shift each character by a set amount, then the shifted value of ‘E’ is likely to be the most frequent, followed by the shifted value of the letter ‘T’ etc.
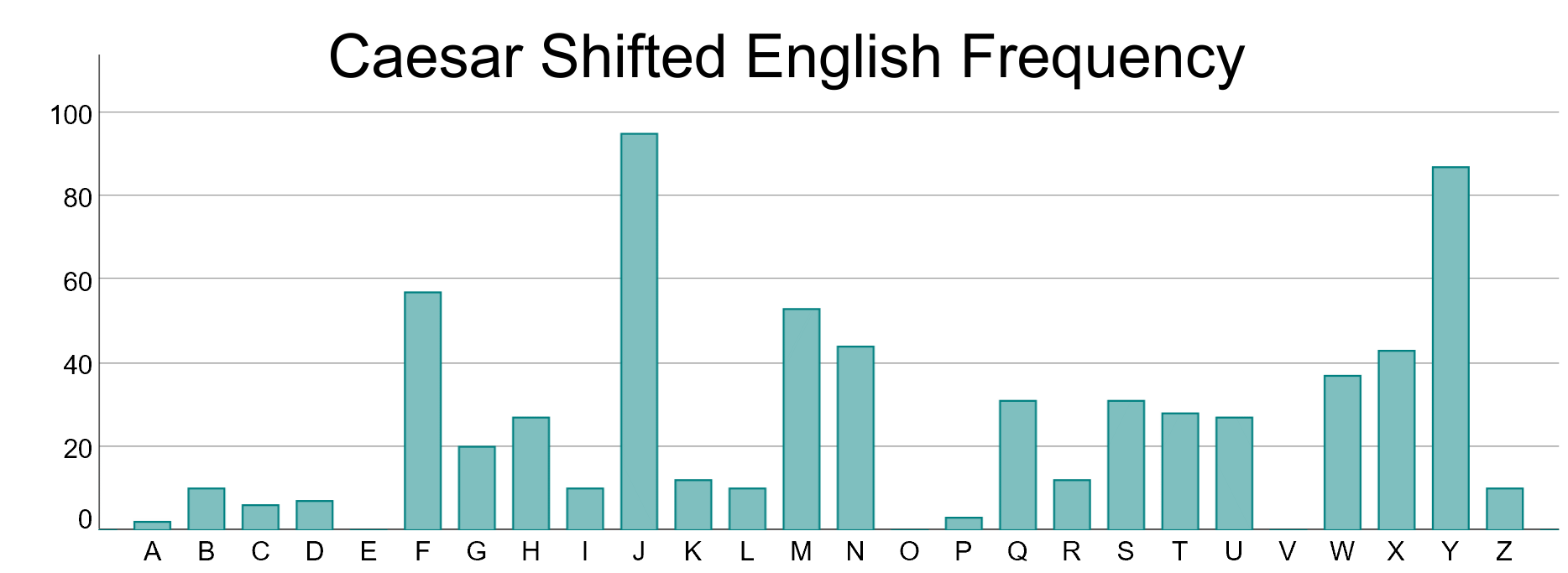We only need to have an educated guess as to what one character has been shifted by, to discover the key used.
Affine shift ciphers
A slightly more secure class of ciphers uses affine transformations of the form \(x\mapsto ax+b\) \(\text{mod}~(26)\), for various integers \(a\) and \(b\).
To decipher successfully, we need to be able to recover the value of \(x\) uniquely from \(ax+b\). More precisely we need to know that if \(ax+b\equiv ay+b\) \(\text{mod}~26\) then \(x\equiv y\) \(\text{mod}~26\).
In the language of functions we want the affine transformation \(f:\mathbb Z_{26}\longrightarrow \mathbb Z_{26}\) defined by the rule \(x\mapsto ax+b\) to be one to one, or injective.
If we take \(a=5, b=3\) we have
ATTACK TOMORROW \(\to\) DUUDNB UVLVKKVJ
When is an affine shift injective?
Suppose that \(ax+b\equiv ay+b\) \(\text{mod}~26\). Then, subtracting \(b\) from both sides we see that \(ax\equiv ay\) \(\text{mod}~26\), and so \(a(x-y)\equiv 0\) \(\text{mod}~26\). This equation has the obvious solution \(x=y\), and if \(a\) is coprime to \(26\), then this is the only solution, since we may cancel the unit \(a\). If on the other hand \(a\) is not a unit, then \(\gcd(a,26)=d>1\) and we may choose \(r\) such that \(rd=26\) and \(s\) such that \(a=sd\). Now it is clear that \(ra=rds=26s\equiv 0\) \(\text{mod}~26\), and so for any \(x\) there is a \(y=x-r\) such that \(a(x-y)=ar\equiv 0\) \(\text{mod}~26\), yielding a second solution to the equation.
We conclude that the affine shift is injective if and only if \(a\) is a unit \(\text{mod }(26)\).
By counting the pairs \(a, b\) we see that there are \(\phi(26)\times26=12\times26=312\) such ciphers. Breaking such a cipher by trying all the possibilities for \(a\) and \(b\) would be tedious by hand (though simple with a computer), but again frequency searches can make the task much easier.
If the enciphering transformation is \(x\mapsto 7x+3 \text{ mod }(26)\), encipher GAUSS and decipher MFSJDG.