8.1 Deciphering the Vigenère cipher

Now that we know how a Vigenère cipher works, how do we attack the cipher?

At first sight, frequency analysis doesn’t seem to be any use to us. However, notice that if we knew the length of the keyphrase, we could reconstruct the columns above (using the ciphertext) and use frequency analysis to determine the key letter used for each column. So all we have to do is learn the length of the keyphrase.

There are two common techniques for this.

Kasiski Test

The idea, put forward independently by Babbage and Kasiski, is that in a large piece of plaintext, it may happen that some common words, or groups of letters, may appear a number of times starting at the same column in the columnar description above. If this is the case, the distance between these words will be a multiple of the length of the keyphrase. Some of these occurrences will of course be purely random but some may not. Hence we look for some common groups of letters in the ciphertext and determine the distance between them. This will give us clues to the length of the keyphrase.

Consider the previous example of a Vigenère cipher

CCGGR UKNKL OJWEX GNZWS GSEJC RWAMG NYVWP CCCIV EREHP WTKGR MFADG SWSGV YIXZT YGLIL TVTTL STZUT LJEVR LEUEJ HUVLH VTDSO NKJEE DPYCB ILCIA PXGGI CPLWR JQFXW NKJIR CIEVE VESFH TLWPC CIRLE OVAPH HRDEX SSSGI RYTYG APHHR DEXMS VFTSO RZVEX ZEFTI KANRN MIKSR IEEFD KJEGA PYGRX WXKCL TZASG TEKBV KNKLH VNEXL EIUTL STRTE WMBJV IXMTV FIRHL REESX TYGPP SIENE XLEIU WLWNK JETDA ZPTIP TRNPL SBVVI WHLRE EHSBF XEXZE TKPLW RKGXX SLGJA FWTRU SLGWE DEPGW ZVIWU LVCRX GSVGT LSTKJ EGAPY GRXWX KCLTZ ASGTL SSSGE RKHZH TIVBP VHVWE GNAGW SYGNG WTYKS JGRDQ FWMBJ VIXMT ZQNMK OWVER UACNE HLHVE AIKAI UHMXT TKPLW RREIT ZEIKS XZEEC MIYIM GNXGA EAFSJ MFHCV QPKQG VSPYK CWMBJ VIXMT ZQNMF WYKCL WATJL ILTVT IWJEG NAGWD SAARG TYGRP WTKGR SJSPO BSDTY KSXWX KKSXS KVPFV GMYVT TOWNU IQGNJ KNKZN VVTLW BCCCO UHROB IJCRG SEJHK OL

We have the following collection of ‘words’ of length 3 and their relative distances apart.

Substring	Positions	Intervals
KNK	7,241,631	234,390
NKL	8,242	234
WSG	19,57	38
GSE	21,655	634
WPC	34,148	114
PCC	35,149	114
CCC	36,642	606
CCI	37,150	113
VER	40,463	423
PWT	45,585	540
WTK	46,586	540
TKG	47,587	540
KGR	48,588	540

Now take these intervals and calculate their greatest common divisors. The keylength is likely to be a divisor of one of these numbers.

\[ \begin{array}{c|llllllll} &234&390&38&634&114&606&423&540\\\hline 234&&78&2&2&6&6&9&18\\ 390&&&2&2&6&6&3&30\\ 38&&&&2&38&2&1&2\\ 634&&&&&2&2&1&2\\ 114&&&&&&6&3&6\\ 606&&&&&&&3&6\\ 113&&&&&&&1&1\\ 423&&&&&&&&9\\ \end{array} \] The values of \(2\) and \(6\) look likely candidates for the keylength.

Once we have determined the keylength, then we can use frequency analysis on each column to try to determine which shift was used. We shall look into this in more details later.

The index of coincidence is a way to measure how close to being English a particular piece of text is. It relies on frequency analysis and a longer explanation of it can be found later, (see 8.2). The important property for us is that it is invariant under a simple substitution cipher such as a Caesar shift. Essentially we try different values for the keyword length and measure how close to being English the corresponding text in each column is. The highest value is likely to be (a multiple of) the column length.

For example, for the ciphertext

we can compute the Index for different values of keyphrase length and get

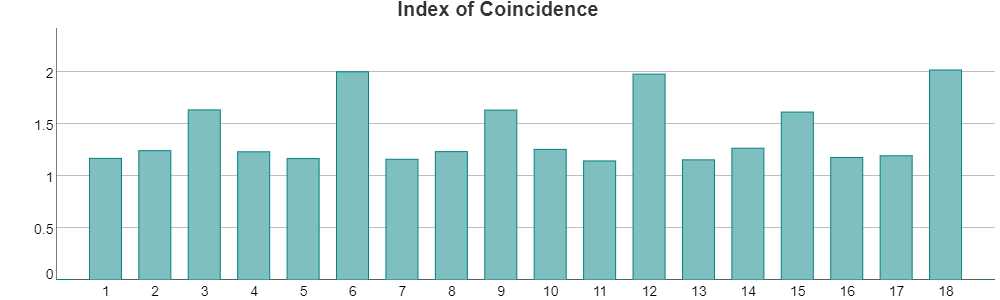This has ‘spikes’ at 6, 12 and 18 suggesting that the keyword might have length 6. Frequency analysis on each of the 6 columns would then yield the plaintext.