Write a function trapez(f, a, b, n):
Background: The equation below shows that the integral I of the function
f(x) from x=a to x=b can be approximated by A through
the so-called composite trapezoidal integration rule:

where h=(b-a)/n, xi=a+i*h, and n is the number of subdivisions.
Example:
The figure demonstrates the idea for f(x)=x2:

The composite trapezoidal rule computes the area under the red line
exactly, where the red line is an approximation of the actual
function of interest (here f(x)=x2) shown by a black dashed line.
Exercise:
Write a function trapez(f, a, b, n) which is given
- a function f which depends on one parameter (i.e. f(x))
- an lower (a) and upper (b) integration limit
- and the number of subdivisions (n) to be used.
The function should use the composite trapezoidal rule to compute
A and return this value.
Examples
In [ ]: def f(x):
...: return x
...:
In [ ]: trapez(f, 0, 1, 1)
Out[ ]: 0.5
In [ ]: trapez(f, 0, 1, 5)
Out[ ]: 0.5
In [ ]: def f2(x):
...: return x * x
...:
In [ ]: trapez(f2, 0, 1, 1)
Out[ ]: 0.5
In [ ]: trapez(f2, 0, 1, 10)
Out[ ]: 0.3350000000000001
In [ ]: trapez(f2, 0, 1, 100)
Out[ ]: 0.33335000000000004
In [ ]: trapez(f2, 0, 1, 1000)
Out[ ]: 0.33333349999999995
Background: In this part of the practical, we
work with simple
cryptographic codes.
Imagine Alice wants to
send a secret message to
Bob and does not want
third parties to be able to understand the message. Here, we imagine that
Alice and Bob can agree on a particular code before they need to exchange
messages.
Alice and Bob will use the same key to (i) encode a message (i.e. change from plain text to something less readable) and later (ii) decode the encoded message back into plain text. This is known as Symmetric-key cryptography, where the same key is used both for encryption and decryption. The image below shows this schematically. The "encoded" message is called "cyphertext" in the image, and the code used for encoding and decoding is the "shared secret key".
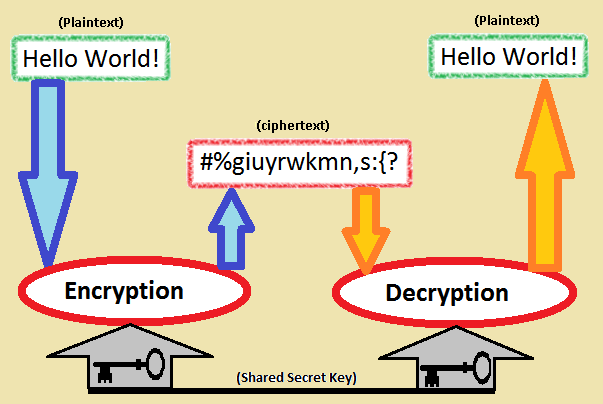
A code in this lab is a mapping that takes an (input) letter of the
alphabet and maps it to a different (output) letter. We can
represent such a code in Python through a dictionary where the keys
of the dictionary are the input characters and the values the
output characters.
For example, let's consider the trivial code that replaces the
letter 'e' in the input data with the letter 'x' in the output, and
simultaneously replaces the letter 'x' in the input data with the
letter 'e' in the output. This could be written as e->x and x->e.
This can be represented by the dictionary
{'x': 'e', 'e': 'x'}. The function code1 provides
exactly this dictionary:
In [ ]: mycode = code1()
In [ ]: print(mycode)
{'x': 'e', 'e': 'x'}
We use the convention that if a character is not found in the keys of the dictionary, the character should not be changed by the code.
We now encode the string Hello World using the mapping described by mycode, and obtain the string Hxllo World.
(If we want to encode information without losing data, we need to
make sure that no two keys map to the same value, i.e. the mapping
has to be injective. Later, we want to reverse the mapping -- to
decode a coded message -- and will need that the mapping has to
be bijective, i.e. there has to be a one-to-one correspondence
between input and output sets.)
Exercise: Write a function encode(code, msg) which takes the arguments:
- code: this is a dictionary describing a code
- msg: this is a string
The function should apply the mapping to each character of the string as described above and return the encoded output string.
Examples
In [ ]: code = code1()
In [ ]: print(code)
{'x': 'e', 'e': 'x'}
In [ ]: encode(code, "Hello World")
Out[ ]: 'Hxllo World'
In [ ]: encode(code, "Jimi Hendrix")
Out[ ]: 'Jimi Hxndrie'
In [ ]: encode(code, "The name xenon (Xe) is derived from greek for strange.")
Out[ ]: 'Thx namx exnon (Xx) is dxrivxd from grxxk for strangx.'
The sentence "the quick brown fox jumps over the lazy dog"
contains all letters of the English alphabet, and might be useful
here as an example:
In [ ]: msg = "the quick brown fox jumps over the lazy dog"
In [ ]: encode(code1(), msg)
Out[ ]: 'thx quick brown foe jumps ovxr thx lazy dog'
The training9.py file provides other codes, for example
code2 which maps i->s, s->g and g->i:
In [ ]: code2()
Out[ ]: {'g': 'i', 'i': 's', 's': 'g'}
In [ ]: encode(code2(), msg)
Out[ ]: 'the qusck brown fox jumpg over the lazy doi'
The code provided by function code3 makes the encoded message fairly unreadable:
In [22]: print(code3())
{'!': '?', ' ': '$', '#': '.', '$': ' ', '.': '#', '?': '!', 'A': 'B', 'C': 'D',
'B': 'C', 'E': 'F', 'D': 'E', 'G': 'H', 'F': 'G', 'I': 'J', 'H': 'I', 'K': 'L',
'J': 'K', 'M': 'N', 'L': 'M', 'O': 'P', 'N': 'O', 'Q': 'R', 'P': 'Q', 'S': 'T',
'R': 'S', 'U': 'V', 'T': 'U', 'W': 'X', 'V': 'W', 'Y': 'Z', 'X': 'Y', 'Z': 'A',
'a': 'b', 'c': 'd', 'b': 'c', 'e': 'f', 'd': 'e', 'g': 'h', 'f': 'g', 'i': 'j',
'h': 'i', 'k': 'l', 'j': 'k', 'm': 'n', 'l': 'm', 'o': 'p', 'n': 'o', 'q': 'r',
'p': 'q', 's': 't', 'r': 's', 'u': 'v', 't': 'u', 'w': 'x', 'v': 'w', 'y': 'z',
'x': 'y', 'z': 'a'}
In [23]: msg
Out[23]: 'the quick brown fox jumps over the lazy dog'
In [24]: encode(code3(), msg)
Out[24]: 'uif$rvjdl$cspxo$gpy$kvnqt$pwfs$uif$mbaz$eph'






