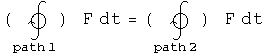Using This Last Definition, Show That Central Forces Are Conservative
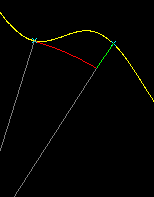To demonstrate that a central force
is conservative consider two points out in space and a
small test mass moving from one to the other along some arbitrary
path. Any point on that path may be reached from any other point
by a combination of motion along a circular arc centered on the
origin, and motion along a radius from the origin.
The arbitrary path we have could be approximated by dividing it
as finely as we wish into arcs and radial movement. Now consider
the work done against a central force with its center at the
origin. Remember that the work done against the force is the
negative of the work done by the force.
Along the circular arc parts of the path, the work is zero
since the motion is perpendicular to the force. In the
radial direction the work done against the force is positive when
the direction of motion is outward from the center and negative
when the direction of motion is inward. So, whatever the path,
the net work done depends only on the difference in distance from
the force center to the path end points. This is because the net
radial displacement is the only component contributing to the
work. So we have demonstrated that all central forces are
conservative. Therefore gravity must be a conservative force.
(*) The curl is the commutator of the differential operator and the force.
