ESTIMATING THE POPULATION MEAN

C. Patrick Doncaster

Whenever you collect a sample of measurements, you will want to summarise its defining characteristics. If the data are approximately normally distributed around some central tendency, and many types of biological data are, then three parametric statistics can provide much of the essential information. The sample mean, , tells you what is the average measurement from your sample; the standard deviation (SD) tells you how much variation there is in the in the data around the sample mean; the standard error (SE) indicates the uncertainty associated with viewing the sample mean as an estimate of the mean of the whole population, .

Parameter		Description	Example
1.	Variable	A property that varies in a measurable way between subjects in a sample.	Weight of seeds of the Princess Bean Phaseolus vulgaris (in: Samuels, M.L. 1991. Statistics for the Life Sciences. Macmillan).
2.	Sample	A collection of individual observations selected by a specified procedure. In most cases the sample size is given by the number of subjects (i.e. each is measured once only).	A sample of 25 Princess Bean seeds, selected at random from the total production of an arable field.	WEIGHT (mg) 343,755,431,480,516,469,69 4,659,441,562,597,502,612, 549,348,469,545,728,416,53 6,581,433,583,570,334
3.	Sample mean	The sum of all observations in the sample, divided by the size of the sample, N. The sample mean is an estimate of the population mean, ("mu") which is one of two parameters defining the normal distribution (the other is , see below).	The sample mean This comes from a population, the total production of the field, which follows a normal distribution and has a mean = 500 mg.
4.	Sum of squares, SS	The squared distance between each data point (Yi) and the sample mean, summed for all N data points.	The sample sums of squares
5.	Variance, v,	The variance in a normally distributed population is described by the average of N squared deviations from the mean. Variance usually refers to a sample, however, in which case it is calculated as the sum of squares divided by N-1 rather than N.	The sample variance v = SS / (N - 1) = 12,928
6.	Sample standard deviation, SD, s	Describes the dispersion of data about the mean. It is equal to the square root of the variance. For a large sample size, = , and the standard deviation of the sample approaches the population standard deviation, ("sigma"). It is then a property of the normal distribution that 95% of observations will lie within 1.960 standard deviations of the mean, and 99% within .	The sample standard deviation s = = 113.7 mg The standard deviation of the population from which the sample was drawn is = 120 mg.
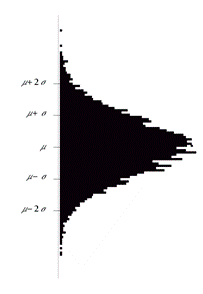
7.	Normal distribution	A bell-shaped frequency distribution of a continuous variable. The formula for the normal distribution contains two parameters: the mean, giving its location, and the standard deviation, giving the shape of the symmetrical 'bell'. This distribution arises commonly in nature when myriad independent forces, themselves subject to variation, combine additively to produce a central tendency. Many parametric statistics are based on the normal distribution because of this, and also its property of describing both the location (mean) and dispersion (standard deviation) of the data. Since dispersion is measured in squared deviations from the mean, it can be partitioned between sources, permitting the testing of statistical models.	The weights of Princess Bean seeds in the population follows a normal distribution (shown in the graph, with frequency on the horizontal axis). Some 95% of the seeds are within 1.96 standard deviations of the mean, which is= 500 235 mg.
8.	Standard error of the mean, SE	Describes the uncertainty, due to sampling error, in the mean of the data. It is calculated by dividing the standard deviation by the square root of the sample size (), and so it gets smaller as the sample size gets bigger. In other words, with a very large N, the sample mean approaches the population mean. If random samples of N measurements were taken from any population (not necessarily normal) with mean and standard deviation , the mean of the sampling distribution of would equal the population mean . Moreover, the standard deviation of sample means around the population mean would be given by .	The standard error of the mean
9.	Confidence interval for	Regardless of the underlying distribution of data, the sample means from repeated random samples of size n would have a distribution that approached normal for large n, with 95% of sample means at. With only one sample mean and standard error SE, these can nevertheless be taken as best estimates of the parametric mean m and standard deviation of sample means. It is then possible to compute 95% confidence limits for at (for large sample sizes). For small sample sizes, The 95% confidence limits for are computed at .	The 95% confidence intervals for m from the sample of 25 Princess Bean seeds are at: = 526.1 2.069 22.74 = 526.1 47.05. The sample is thus representative of the population mean, which we happen to know is 500 mg. If we didn't know this, the sample would nevertheless lead us to accept a null hypothesis that the population mean lies anywhere between 479.05 and 573.15 mg.