|
||
| P=8 | ||
| Diameter | 7 | P-1 |
| Valency | 2 | 2 |
| d×v | 14 | 2(P-1) |
| Bisection Bandwidth | B | B |
 |
||
| P=16 | ||
| Diameter | 6 | 2(P1/2-1) |
| Valency | 4 | 4 |
| d×v | 24 | 8(P1/2-1) |
| Bisection Bandwidth | 4B | P1/2B |
 Hidden nodes and associated links not shown. |
||
| P=64 | ||
| Diameter | 9 | 3(P1/3-1) |
| Valency | 6 | 6 |
| d×v | 54 | 18(P1/3-1) |
| Bisection Bandwidth | 16B | P2/3B |
Grids of greater than 3 dimensions are unlikely to be encountered.
| Diameter | N(P1/N-1) |
| Valency | 2N |
| d×v | 2N2(P1/N-1) |
| Bisection Bandwidth | P(N-1)/NB |
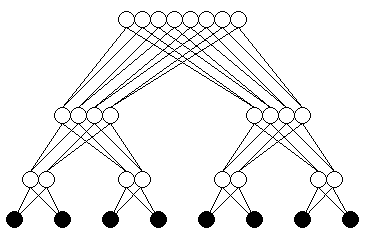
A binary tree is one in which each non-leaf node has two children.
 |
||
| P=15 | ||
| Diameter | 6 | 2log2((P+1)/2) |
| Valency | 3 | 3 |
| d×v | 18 | 6log2((P+1)/2) |
| Bisection Bandwidth | B | B |
Note that ((P+1)/2) is the number of leaf nodes.
In a ternary tree each non-leaf node has three children.
 |
|
| P=13 | |
| Diameter | 4 |
| Valency | 4 |
| d×v | 16 |
| Bisection Bandwidth | 3B |
Note that the bisection bandwidth gives the impression that this network performs better than it does. In fact it's just difficult to find somewhere to cut it in half.
In a quaternary tree each non-leaf node has four children.
 |
|
| P=21 | |
| Diameter | 4 |
| Valency | 5 |
| d×v | 20 |
| Bisection Bandwidth | 2B |